Atmospheric eddies in Science Centers – connection between secondary school teaching and informal learning
Péter Tasnádi
There are many atmospheric phenomena which can be taught in the frame of different subjects at secondary schools. Geography and environmental education characteristically deal with observable natural phenomena. Some of them can be easily modeled in a school laboratory, but in spite of this neither the exact (phenomenological) description nor the theoretical background of these phenomena are given in any of the curricula. These phenomena include a wide scale of atmospheric and marine whirls. The beauty and frightening effect of the vortices from dust devils and waterspouts to hurricanes and cyclones can be a great motivating force for the students to learn more about the physics of these phenomena. This paper demonstrates the introductory steps of the elaboration of a learning material about the atmospheric eddies and shows how can be connected the formal and non-formal teaching methods. To construct the teaching material the principles of the MER (Model of Educational Reconstruction) will be applied (Niebert and Gropengiesser, 2013), having planned the educational reconstruction of the scientific content we suggest simple conceptual and mathematical description of atmospheric whirls of tornadic type at secondary school level.
Atmosphere and processes occurring in it are very interesting ones and our everyday life is highly influenced by them. Tornadoes and hurricanes are sometimes frightening but always exciting phenomena. There are lots of people who fanatically observe these and take photos and videos from them. In spite of this, mainly due to the complexity of the processes mentioned above, curriculum contains very modestly this field of physics. However, it is not difficult to excite the curiosity of the students by these admirable spectacles. Meteorological data, satellite and radar images of the atmosphere give wide possibility for teachers to set project work for students to do self-sufficient research-work. These topics can be illustrated with beautiful pictures (Fig. 1) which can be downloaded from the internet. Their physical background can be treated at different level depending on the previous experiences of the students. Besides this studying vortices occurring in rotating containers can provide an opportunity for students to understand the role of the forces governing the atmospheric processes – the gravitational force, the Coriolis force, and the friction force – and to work individually under proper supervision.

Figure 1(a) A visible image of Major Hurricane Matthew taken from NASA's Terra satellite on 7 October 2017 at 00:00 EDT as it continued moving along Florida's East Coast. Matthew was a Category 3 hurricane at the time of this image (Credit: NASA's Goddard MODIS Rapid Response Team). (b) A dust devil in Arizona (source: Wikipedia, credit: NASA). (c) A fire whirl at 19 February 2002 (source: Wikipedia, credit: the US Fish and Wildlife Service).
In this paper we deal mainly with dust devils, fire whirls, tornadoes and tropical cyclones. They can be treated more or less in a similar way, but while the first three are of rather small scale and with forces in action which the Coriolis force cannot compete with, the latter is of much larger scale and in some regions of it the Coriolis force plays significant role (see Sect. 4.2.2). This makes tropical cyclones rotating strictly counterclockwise, while the others can rotate both directions.
The atmospheric phenomena can be investigated essentially at three levels. The first level is to classify and analyze the observations and to present model experiments related to the phenomenon investigated. On the next level, we create a conceptual model that helps to understand the phenomenon, and on the third level we construct a precise mathematical model based on the conceptual model. In this paper we examine which parts of the scientific level investigations of the vortices and with what kind of simplifications can be introduced into the education at the secondary school level. This is the first iterative step in the processing of a MER-type educational material, when the selection of some parts and concepts from the scientific description of the phenomena and the selection of the teaching method appropriate to the age of the pupils occurs.
The atmospheric vortices are currently a vividly researched part of meteorology, and there are incredible amount of papers and books about the results. Due to the development of the experimental and measuring technics enormous amount of observation have accumulated about the broad scale of atmospheric eddies. The theoretical description of the vortices has been also improved and the result of the measurements has been verified with high quality simulations too. The theoretical description of vortices is based on the Navier Stokes equation written in non-inertial frame of reference as well as on the laws of the thermodynamics. Their time development can be followed with applying the three dimensional vorticity equations. Calculations need to apply higher mathematics (e.g. partial differential equations, spherical polar coordinates etc.). So in the explanation of the atmospheric vortices both the applied physics laws and mathematics are highly beyond the secondary school level. Therefore teachers should select very cautiously the content knowledge and the mathematics applied when the educational reconstruction is elaborated. To help this, we make recommendations in this article and in the background material to be created later. We have chosen two books (Houze, 1993; Allaby, 2004) and some METED learning materials (Laing and Evans, 2016) as a reference when we have made proposals to the content knowledge of secondary school teaching. We have mainly relied on qualitative findings about the vortices, and tried to create a description fitting well to secondary school level. The following properties of vortices were chosen as basics for this procedure. Their common feature is the central pressure depression about which the air particles are spiralling upwards. Due to the fierce upward motion generally a downward motion is developing in the middle of the whirls. According to in situ and model measurements as well as simulations the core of the whirls is warmer than its environment (Emmons and Ying, 1967; Zhao et al., 2004; Balme and Greeley, 2006; Herrero et al., 2012). The descending air is moving nearly adiabatically therefore it becomes warmer than the air in the wall of the whirl where the air is moving upwards (also nearly adiabatically). The smaller whirls can rotate either clockwise or anticlockwise.
Science centres feature interactive exhibits and offer hands-on experiences for visitors, encouraging them to experiment and explore. Among others, the Dynamic Earth in Edinburgh, UK (https://www.dynamicearth.co.uk/, last access: 18 July 2019), the Universum in Bremen, Germany (https://universum-bremen.de/?lang=en, last access: 18 July 2019), and the Vida Science Centre in Brno, Czech Republic (https://vida.cz/en/, last access: 18 July 2019) has a very wide range of experiments related to hydrodynamics. Vörös and Sárközi (2016) also mention some European science centres featuring environmental physics exhibits. In the following we will introduce two possibilities from Hungary related to the informal teaching of atmospheric eddies.

Figure 2(a) A water whirl in a column of water, initiated by some paddles in the bottom of the vessel – made by the visitor itself (Center of Scientific Wonders). (b) A “tornado” in a rotating vessel filled with water (Kármán Lab, ELTE). The paint dropped into the vessel shows its structure. A short film about this can be found at http://scilwg.elte.hu/2018/EMS/film/6494_75s.wmv (last access: 18 July 2019). (c) A fire whirl, which was shown during an experimental demonstration to the visitors – whirl with and without rotating the plate below the cylindrical wire mesh (Center of Scientific Wonders) (all of these photos by A. Király).
3.1 Science centres and informal learning, the Center of Scientific Wonders in Budapest
The Center of Scientific Wonders in Budapest (it is also known under the name of Palace of Miracles) was the first science center in Eastern-Europe, it has opened its gates 22 years ago. Nowadays we have more than ten science centres in Hungary, some of them are focusing to a narrow topic, e.g. the Mobilis Science Center in Győr to the physics of automobiles and traffic, or the Futura Science Center in Mosonmagyaróvár to sustainability and renewable energy sources.
The Center of Scientific Wonders has got more than 250 games and tools demonstrating various physical (Fig. 2a), chemical and biological phenomena; fascinating lectures and experimental demonstrations (Fig. 2c). They also have some programs for teachers and science educators showing how the science centres can help education, the more to arouse the interest of children and students in natural sciences and engineering. Meteorology related interactive games and science shows have been present in their scientific-educational program from the establishment of the centre. Some months ago they has started a joint event with the experts of The Hungarian Meteorological Service (OMSZ) consisting of monthly live streamed lectures and talks.
3.2 Laboratory visits at the von Kármán environmental flows lab of the University
The Eötvös Loránd University (ELTE) has a research lab, the von Kármán Laboratory for Environmental Flows, which is one of the very few of its kind in Europe. Based on the principles of hydrodynamic similarity, large-scale atmospheric and oceanic phenomena (shallow-water waves, tsunamis, weather fronts, atmospheric convection, cyclones, tornados, etc.) can be accurately modelled and demonstrated here (Fig. 2b) in relatively simple, aquarium-sized experimental setups. This university lab is open for guided tours of visiting groups (preferably high school students) on one day per week (usually on Fridays) at any pre-agreed time. Sometimes they also organize a Lab tour for the public on the Researchers' Nights and other special events of the University. As we mentioned above, the von Kármán Laboratory for Environmental Flows is also a research lab, a nice detailed study about modelling atmospheric vortices was done here by Halász et al. (2007).
The secondary school level treatment of atmospheric eddies is highly restricted by the national physics curriculum. However, curricula permit the discussion of so called additional topics which can be freely chosen by teachers. The atmospheric whirls, due to their impressive appearance, as we have mentioned, are very suitable to be complex additional topics for secondary school physics (Döményné Ságodi et al., 2009). The selection of the knowledge content can be done along the three investigation levels which was already mentioned.
At first students should observe directly and indirectly the phenomena. Taking photographs about whirls and looking for videos about them at the internet arouse their interest. However, according to our experiences students quickly begin to try to find out the explanation of the spectacular phenomena. After observing the phenomena they should collect the experimental facts and data about the mechanical and thermal properties of whirls with the help of their teachers. (Relevant data can be find e.g. Rennó and Bluestein, 2001; Kanak, 2005; Bluestein, 2013).
4.1 Conceptual models
Having got the experimental facts construction of conceptual models are the best tools to give explanations of the intricate motion of the air in the whirls. Conceptual models show a schematic picture of the stream lines which can be regarded as the path of the moving air particles (and dust or water drops).
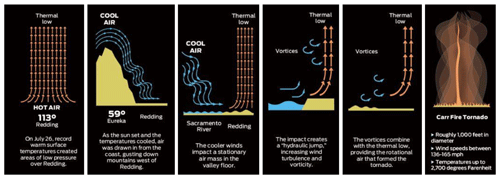
On the basis of this pictures the vortex movement and the three dimensional structure of the whirls can be explained, without the explicit use of the concept of vorticity vector or angular momentum. (At this level it is worth mentioning that atmospheric whirls are visible due to the sucked dust and debris or water droplets.) The models are indicating that a relatively strong convection and the rotation about a vertical axle are necessary requirements of the arising of the tornadic whirls (dust devils, water whirls, fire whirls and tornadoes). These models are the most important part of the knowledge content of the proposed teaching material because they qualitatively reflect the basic features of phenomena and with further simplifications can serve as a starting point for quantitative description. The sequence of drawings in Fig. 3. explain the development of a fire whirl (the so called Carr Fire) happened in July of 2018 in the area of Redding, in California (Johnson, 2018). The formation of the vertical whirls can be explained by the so called hairpin (horseshoe) mechanism (Oncley et al., 2016). According to this mechanism a horizontal vortex line is tilted in vertical direction by a strong updraft coming into existence due to a local warming of the ground. For this reason, two vortices rotating in opposite directions come into existence. Sometimes both of these whirls persist, but usually the anticyclonic one ceases (The formation of supercells is often the consequence of this mechanism too.) The vertical stretching of the fire column is a consequence of the fierce updraft. It is demonstrated very impressive way in a film, where a moving dust devil covers a burning oil-well. (Dust Devil “Firenado” On Russian Gas Field: https://www.youtube.com/watch?v=qg9YCTbO4ag, last access: 18 July 2019).
4.2 Kinematics and dynamics of vortices
The highest level of understanding a phenomenon is the quantitative description. At scientific level this can be done by the use of the suitable form of the Hydro- and Thermodynamic Equations. At secondary school level we have no chance to apply partial differential equations and to use spherical polar coordinates, therefore the atmospheric whirls can be treated only by strong simplification of the conceptual models. However, it will be shown, in spite of the simplifications, that a simple dynamic model supported only by the dynamics of circular motion can provide quantitative results reflecting the important properties of the whirls. Most of atmospheric whirls can be regarded as a rotating air column. The velocity distribution of the vortices stabilizes for a shorter or longer period of time and in this period, according to measurements, the tangential velocities can be approximated with that of a Rankine vortex (Wood and White, 2010). In a first approximation we can ignore the vertical motion of the particles thereby they are moving on horizontal circles.
Table 1The typical values of characteristic velocity (U) and characteristic length (L), the Rossby-number (Ro), and the type of the force balance in the three regions of an intense and a weak tropical cyclone. Based on MetEd (Laing and Evans, 2016).

Dynamically the horizontal motion of the stationary whirls can be described by the radial equation of motion:
where ρ is the density, r is the radial distance from the axle of the column, FΔp, and FCo are the gradient, and the Coriolis force, respectively. The gradient force expresses the effect of the pressure difference at a given place the notation Δp in the index reminds us to this. The analysis of the magnitude of the forces shows that the friction force is generally smaller than the other forces involved therefore, for the sake of simplicity it is neglected. However, the interpretation of the equation, in spite of its simplicity, is not easy. The main difficulty comes from the use of the accelerating coordinate system fixed to the rotating Earth, so inertial forces have to be taken into account. One of the most important didactic question is how the Coriolis force can be introduced at secondary school level. This question is discussed in numerous publication (Higbie, 1980; Wilson, 2011; Gróf, 2016) therefore we do not go into details here. As the best possibility for introducing the Coriolis force we suggest (Tél et al., 2018). We mention furthermore that Eq. (1) is often interpreted in the reference frame of the rotating column. This interpretation causes superfluous difficulties at secondary school level due to the use of two non-inertial frames where one of them is embedded into the other one.
The treatment of the gradient force is also not simple, but we can approximate the derivative of the pressure with the Δp∕Δr difference quotient. The approximation is maybe familiar for student who experienced in computer programming.
4.2.1 The Rossby number
To apply Eq. (1) for the description of tornadic whirls and tropical cyclones we suggest making a simple scale analysis. It is worth writing the
ratio of the centripetal and Coriolis force where v is the speed, r is the radius, and f is the Coriolis parameter, which is slightly depends on the geographical location, but here we regard it as a constant. The value of the Coriolis parameter at the Equator is zero and at the poles is but in a whirl which is at a given place it changes only slightly. Taking into account the characteristic speeds and radii of the dust devils and those of the fire whirls and water whirls we can conclude that the Coriolis force is negligible, so for tornadic type whirls the equation of motion can be simplified to .
The scale analysis of the equation of motion of tornadic whirls and hurricanes can be executed without mentioning the Rossby number. However, it is worth introducing it by the general definition:
where U is the characteristic value of the speed, L is the characteristic length of the motion investigated, and f is the above mentioned Coriolis parameter. The Rossby number is a dimensionless quantity and suitable for the comparison of the magnitude of forces in rotating systems. (Applying the Rossby number at secondary schools the use of dimensionless equations can be also prepared.)
4.2.2 Tropical cyclones
The motion of a hurricane is more complicated. Here we essentially can follow the description which can be found in METED (Laing and Evans, 2016). However, against the METED's interpretation we deliberately don't use the frame rotating together with the air. Although the physical properties of the tornadic whirls and tropical cyclones are very similar, the size of the latter is much bigger so it can be divided into three regions in which, due to the increase of the radius (the characteristic length), the Rossby number indicates the dominance of different forces.
In case of Ro<1 the horizontal motion is geostrophic and FΔp=FCor, (this region is the farthest from the centre of the cyclone) in case of Ro≈1 a gradient wind is developing and , and in case of Ro≫1 the motion is cyclostrophic and Fcp=FΔp, the Coriolis force is negligible (this region is the eye wall area of the hurricane).
It can be seen that the motion of tornadic whirls is cyclostrophic while, tropical cyclones have three regions: Eye, Storm Strength, Outer. As a simple storm analysis we could calculate the Rossby-number for both an intense and a weak tropical cyclone in the three typical regions with using the typical values for the wind speed U and for the spatial scale L, and regarding f as a constant value of , and comparing the resulting values for Ro for each storm in each region, we could see whether the fundamental balances in the regions would change with changing intensity (see in Table 1).
We could conclude even from this simple analysis, that the balance structures of different storms vary with its radius, and the gradient wind region extends further for the intense tropical cyclone than for the weak ones.
The whirls are interesting and spectacular atmospheric phenomena, and their observations and laboratory reproductions are suitable to increase the students' motivation and to raise their interest towards physics and environmental issues. By analysing the properties of the tornadic whirls we made proposals for secondary school teaching of them. The steps of teaching will be the following: observation of the phenomena, making conceptual models, and giving a mathematical description on the basis of simplified conceptual models. The most intricate point of the line of reasoning at secondary school level is the applied reference system and the understanding of the exact meaning of the Coriolis and the pressure gradient force. We strongly recommend the use of the surface of the Earth as reference system. Going to an informal place of education, such as a Science Center or a university lab, or participate in some experimental demonstration event also could make learning physics more enjoyable for the students. Besides this, analysing the physical properties of whirls, students can gain skills in modelling natural phenomena.
The data used can be found in the cited literature.
AK was responsible for the description about Science Centres and other informal learning possibilities, and PT for secondary school level model.
The authors declare that they have no conflict of interest.
This article is part of the special issue “18th EMS Annual Meeting: European Conference for Applied Meteorology and Climatology 2018”. It is a result of the EMS Annual Meeting: European Conference for Applied Meteorology and Climatology 2018, Budapest, Hungary, 3–7 September 2018.
This work has received funding from the Hungarian Academy of Sciences.
This research has been supported by the Content Pedagogy Research Program of the Hungarian Academy of Sciences (grant no. 471027).
This paper was edited by Tomas Halenka and reviewed by two anonymous referees.
Allaby, M.: Tornadoes, Rev. Edn., Facts on File Inc., New York, NY, 2004.
Balme, M. and Greeley, R.: Dust devils on Earth and Mars, Rev. Geophys., 44, RG3003, https://doi.org/10.1029/2005RG000188, 2006.
Bluestein, H. B.: Severe Convective Storms and Tornadoes, Springer-Verlag, Berlin, Heidelberg, 2013.
Döményné Ságodi, I., Tasnádi, P., and Nagy, P.: Atmospheric physics as a tool for making physics more interesting for students, in: MPTL 14: International Workshop on Multimedia in Physics Teaching and Learning, paper: T3_81_OP, edited by: Michelini, M., University of Udine, Udine, Italy, 2009.
Emmons, H. W. and Ying, S.-J.: The fire whirl, Int. Sympos. Combust., 11, 475–488, https://doi.org/10.1016/S0082-0784(67)80172-3, 1967.
Gróf, A.: Carousels to Coriolis. What did you learn in geography?, in: Teaching Physics Innovatively – New Learning Environments and Methods in Physics Education, e-book, edited by: Király, A. and Tél, T., ELTE Eötvös Loránd University, Budapest, Hungary, 119–124, ISBN 978-963-284-815-0, 2016.
Halász, G., Gyüre, B., Jánosi, I. M., Szabó, K. G., and Tél, T.: Vortex flow generated by a magnetic stirrer, Am. J. Phys., 75, 1092–1098, 2007.
Herrero, H., Navarro, M. C., and Pla, F.: Influence of Horizontal Temperature Gradients on Convective Instabilities with Geophysical Interest, in: Advanced Fluid Dynamics, edited by: Hyoung Woo Oh, InTech, Rijeka, Croatia, 81–94, ISBN 978-953-51-0270-0, 2012.
Higbie, J.: Simplified approach to Coriolis effect, Physics Teacher, 18, 459–460, https://doi.org/10.1119/1.2340567, 1980.
Houze Jr., R. A.: Cloud Dynamics, Academic Press, An Imprint of Elsevier, Oxford, 1993.
Johnson, L.: 150 Minutes of Hell. The inside story of death and survival as the Carr Fire's tornado of flames stormed Redding – and changed firefighting in a warming California, San Francisco Chronicle, 5 December 2018, Updated: 12 December 2018, available at: https://projects.sfchronicle.com/2018/carr-fire-tornado/ (last access: 9 January 2019), 2018.
Kanak, K. M.: Numerical simulation of dust devil-scale vortices, Q. J. Roy. Meteorol. Soc., 131, 1271–1292, https://doi.org/10.1256/qj.03.172, 2005.
Laing, A. and Evans, J.-L.: Introduction to Tropical Meteorology, in: 2nd Edn., A Comprehensive Online & Print Textbook (Version 4.0, Marc 2016), Produced by The COMET® Program, University Corporation for Atmospheric Research, available at: https://www.meted.ucar.edu/tropical/textbook_2nd_edition/ (last access: 9 January 2019), 2018.
Niebert, K. and Gropengiesser, H.: The model of educational reconstruction: A framework for the design of theory based content specific interventions. The example of climate change, in: Educational design research – Part B: Illustrative cases, edited by: Plomp, T. and Nieveen, N., Enschede, the Netherlands, 511–531, 2013.
Oncley, S. P., Hartogensis, O., and Tong, C.: Whirlwinds and Hairpins in the Atmospheric Surface Layer, J. Atmos. Sci., 73, 4927–4943, https://doi.org/10.1175/JAS-D-15-0368.1, 2016.
Rennó, N. O. and Bluestein, H. B.: A Simple Theory for Waterspouts, J. Atmos. Sci., 58, 927–932, 2001.
Tél, T., Kadi, L., Jánosi, I. M., and Vincze, M.: Experimental demonstration of the water-holding property of three-dimensional vortices, Eur. Phys. Lett., 123, 44001, https://doi.org/10.1209/0295-5075/123/44001, 2018.
Vörös, A. and Sárközi, Z.: Promoting environmental physics issues in science centers and at science-events, in: Teaching Physics Innovatively – New Learning Environments and Methods in Physics Education, e-book, edited by: Király, A. and Tél, T., ELTE Eötvös Loránd University, Budapest, Hungary, 79–84, ISBN 978-963-284-815-0, 2016.
Wilson, A. E.: Jogging on a Carousel, Physics Teacher 49, 570–571, https://doi.org/10.1119/1.3661105, 2011.
Wood, V. T. and White, L. W.: A New Parametric Model of Vortex Tangential-Wind Profiles: Development, Testing, and Verification, J. Atmos. Sci., 68, 990–1006, https://doi.org/10.1175/2011JAS3588.1, 2010.
Zhao, Y. Z., Gu, Z. L., Yu, Y. Z., Ge, Y., Li, Y., and Feng, X.: Mechanism and large eddy simulation of dust devils, Atmos.-Ocean, 42, 61–84, https://doi.org/10.3137/ao.420105, 2004.
- Abstract
- Introduction
- Scientific background
- Atmospheric eddies in Science Centres and at other non-formal places of education
- What can be said at secondary school level
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Scientific background
- Atmospheric eddies in Science Centres and at other non-formal places of education
- What can be said at secondary school level
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References