Teleconnections and Extreme Ocean States in the Northeast Atlantic Ocean
Colm Clancy
Laura Zubiate
Jelena Janjić
Sarah Gallagher
Frédéric Dias
The Northeast Atlantic possesses an energetic and variable wind and wave climate which has a large potential for renewable energy extraction; for example along the western seaboards off Ireland. The role of surface winds in the generation of ocean waves means that global atmospheric circulation patterns and wave climate characteristics are inherently connected. In quantifying how the wave and wind climate of this region may change towards the end of the century due to climate change, it is useful to investigate the influence of large scale atmospheric oscillations using indices such as the North Atlantic Oscillation (NAO), the East Atlantic pattern (EA) and the Scandinavian pattern (SCAND). In this study a statistical analysis of these teleconnections was carried out using an ensemble of EC-Earth global climate simulations run under the RCP4.5 and RCP8.5 forcing scenarios, where EC-Earth is a European-developed atmosphere ocean sea-ice coupled climate model. In addition, EC-Earth model fields were used to drive the WAVEWATCH III wave model over the North Atlantic basin to create the highest resolution wave projection dataset currently available for Ireland. Using this dataset we analysed the correlations between teleconnections and significant wave heights (Hs) with a particular focus on extreme ocean states using a range of statistical methods. The strongest, statistically significant correlations exist between the 95th percentile of significant wave height and the NAO. Correlations between extreme Hs and the EA and SCAND are weaker and not statistically significant over parts of the North Atlantic. When the NAO is in its positive phase (NAO+) and the EA and SCAND are in a negative phase (EA−, SCAND−) the strongest effects are seen on 20-year return levels of extreme ocean waves. Under RCP8.5 there are large areas around Ireland where the 20-year return level of Hs increases by the end of the century, despite an overall decreasing trend in mean wind speeds and hence mean Hs.
The Northeast Atlantic has an energetic, variable wind and wave climate with a significant potential for renewable energy applications (Gallagher et al., 2013, 2016b; Atan et al., 2016). Global atmospheric circulation patterns and wave climate characteristics are inherently connected through the role of surface winds in the generation of ocean waves. Several previous studies have shown strong correlations between the wave climate of the North Atlantic Ocean and atmospheric teleconnection patterns such as the North Atlantic Oscillation (NAO) and the East Atlantic teleconnection pattern (EA) (for example, Barnston and Livezey, 1987; Wang and Swail, 2001, 2002; Charles et al., 2012; Bertin et al., 2013; Dodet et al., 2010; Atan et al., 2016; Santo et al., 2016a). The Scandinavian teleconnection pattern (SCAND) and East Atlantic Western Russian (EA/WR) pattern are other modes of Northern Hemisphere atmospheric variability, and along with the EA have a weaker, but nevertheless significant, influence on the North Atlantic than the NAO (Santo et al., 2016b). In particular, the EA and SCAND have been found to have an impact on the relationship between the NAO and European precipitation patterns (Comas-Bru and McDermott, 2014), and wind energy resources (Zubiate et al., 2017) in winter, by modulating the location and relative intensity of the NAO centres of action.
A strong link between low-frequency modes of atmospheric variability and mean significant wave height (Hs), wave period and peak direction of the waves in Irish coastal waters was identified by Gallagher et al. (2014). The influence of the NAO on extreme sea states in the Northeast Atlantic Ocean was investigated by Gleeson et al. (2017) explaining how this may change in the future using an ensemble of WAVEWATCH III (Tolman, 2014) simulations driven by output from the Coupled Model Intercomparison Project 5 (CMIP5) (Taylor et al., 2012) climate simulations carried out using the EC-Earth (Hazeleger et al., 2010, 2012) global climate model.
The Gleeson et al. (2017) study focused on the NAO, which is the leading mode of atmospheric variability in the North Atlantic region and is manifested as a meridional dipole in mean sea-level pressure (MSLP), with centres of action over Iceland and the Azores (Hurrell, 1996; Greatbatch, 2000; van Loon and Rogers, 1978). Variations in the amplitude and phase of the NAO are linked to changes in the intensity and frequency of storms and blocking patterns (Scherrer et al., 2006). A positive NAO phase is associated with a stronger pressure gradient over the North Atlantic, stronger westerly winds and larger waves. On the other hand, a negative NAO phase is associated with a weaker pressure gradient, slacker winds and smaller waves. Gleeson et al. (2017) showed that the 95th percentile of Hs is strongly positively correlated to the NAO, where the station-based interpretation of NAO was employed. Projections of Hs extremes were found to be location dependent; under the influence of positive NAO, the return levels of Hs may increase in the future despite the overall decreasing trend in the projections of Hs.
The most commonly used calculation of the NAO index uses the station-based definition which involves the difference between MSLP anomalies in the Icelandic Low and Azores High action regions (Hurrell, 1996; Pokorná and Huth, 2015). This definition was used in Gleeson et al. (2017) and applied to the EC-Earth gridded MSLP fields (using the nearest grid point to the location of interest). Disadvantages of this method are that it is fixed in space and shows low signal-to-noise ratios.
An alternative method for deriving the NAO index involves calculating the principal component (PC) time series of the leading empirical orthogonal function (EOF) of gridded MSLP or 500 hPa geopotential height fields spanning an area bounded by 20–90∘ N and 80∘ W–40∘ E. Note that this method is particularly sensitive to the spatial domain and time period used. The PC of the second leading EOF is usually the East Atlantic (EA) pattern which has a centre of action in the Atlantic Ocean west of Ireland; the third leading mode is usually the Scandinavian (SCAND) pattern. However, these modes often account for approximately the same percentage of atmospheric variability and thus the second and third EOFs often interchangeably correspond to either the EA or SCAND and are identifiable using a plot of the particular 2-D EOF.
The study presented in this paper extends the analysis of Gleeson et al. (2017). Here we include the three most dominant modes of northern hemisphere atmospheric variability – the NAO, the EA and the SCAND and employ the EOF analysis method in their calculation. The analysis was carried out for the following North Atlantic area 20–90∘ N 80∘ W–40∘ E using a 3-member ensemble of historical and RCP4.5/8.5 projection EC-Earth data for the months of December to March. It is important to note that our ensemble size is small. This was due to the computational demands required to run the very high resolution wave simulations.
The EA was first described by Wallace and Gutzler (1981). It is defined by a centre of positive 500 hPa height anomalies around the subtropical North Atlantic. It is known to play a role, with the NAO, in determining the latitude and extent of the jet stream, and therefore, the main Atlantic storm track (Woollings and Blackburn, 2012). In its negative phase (negative MSLP anomalies in the mid Atlantic) the EA is known to contribute to northwest swells in the Bay of Biscay (Izaguirre et al., 2010).
The SCAND was defined by Barnston and Livezey (1987) as the Eurasia-1 pattern. It is characterised by high pressure anomalies over the Scandinavian Peninsula and a more diffuse centre of opposite sign over Greenland. It corresponds to the Scandinavian blocking regime identified in anticyclonic set-ups, and is associated with colder than average winter temperatures and higher occurrences of easterly winds over Western Europe (Vautard, 1990). This pattern is known to be negatively correlated with wind speeds and significant wave heights during at least the extended winter months (Trigo et al., 2008).
The paper is organised as follows: Sect. 2 provides details about the EC-Earth and WAVEWATCH III models used in this study. The atmospheric teleconnections are described in more detail in Sect. 3. In Sect. 4 the results of the various statistical tests are presented and discussed. Conclusions on the findings of this study are presented in Sect. 5.
The work presented in this paper used data from CMIP5 (Taylor et al., 2012) simulations carried out using version 2.3 of the EC-Earth (Hazeleger et al., 2010, 2012) global climate model to drive the WAVEWATCH III wave model (Tolman, 2014). Details on each of these models are provided in Gleeson et al. (2017) but a summary is repeated here for completeness.
2.1 EC-Earth climate simulations
The EC-Earth global climate model used for the CMIP5 climate simulations consists of an atmosphere-land surface module coupled to an ocean-sea ice module (Hazeleger et al., 2010, 2012). The atmospheric component of the model was based on the European Centre for Medium-Range Weather Forecasts (ECMWF) Integrated Forecasting System (horizontal resolution of 1.125∘ or approximately 125 km and 62 vertical layers up to 5 hPa). The Nucleus for European Modelling of the Ocean (NEMO) version 2 was used for the oceanic component (Madec, 2008) with an average horizontal resolution of 1∘ (approximately 110 km) and 42 vertical levels. The sea-ice component was the Louvain-la-Neuve Sea Ice Model (LIM) version 2 (Fichefet and Maqueda, 1997). The Ocean Atmosphere Sea Ice Soil coupler (OASIS) version 3 (Valcke, 2006) was used to couple the atmosphere-land surface module with the ocean-sea ice module.
The EC-Earth CMIP5 climate simulations span the period 1850 to 2100. The years 1850 to 2009 are classified as the historical period and included observed greenhouse gases and aerosol concentrations such as black carbon and volcanic eruptions. The future period span from 2006 to 2100 under both RCP4.5 and RCP8.5 CMIP5 climate forcing scenarios. 3 of the 14 EC-Earth CMIP5 ensemble members were generated by Met Éireann and available for use in generating the high resolution wave dataset for Ireland. The EC-Earth ensemble does not have a large spread in terms of annual mean wind speeds and the three Met Éireann ensemble members encapsulate the range of interannual variability.
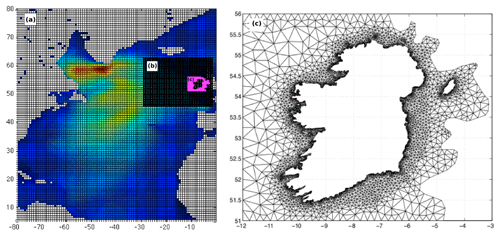
Figure 1(a–c) The three wave model grids as described in Gallagher et al. (2016a). (a) The large North Atlantic grid has a resolution. (b) The grid for the Northeast Atlantic has a resolution. Right panel (c) The wave model unstructured grid around Ireland has a resolution ranging from 15 km offshore to 1 km in the nearshore characterised by 4473 nodes.
2.2 WAVEWATCH III simulations
WAVEWATCH III is a third-generation “phase-averaged” model based on a stochastic representation of the sea surface solving the wave-action balance equation (Komen et al., 1994). The evolution of the wave energy spectrum in the presence of currents and bathymetry is described through the conservation of action density (advection and refraction), which is balanced by source terms (Janssen, 2008). The dissipation and source term parameterisations formulated in Ardhuin et al. (2010) were used in this study.
EC-Earth 10 m wind speeds and sea-ice fields (Gleeson et al., 2013) were used to drive the ensemble of nested regional wave projections over the North Atlantic (see Fig. 1). The outermost grid was a regular grid of resolution over the North Atlantic; the second grid covered part of the Northeast Atlantic on a regular grid and the innermost grid centred around Ireland was unstructured (Roland, 2008) with a resolution of approximately 15 km at the grid boundaries increasing to 1 km in the nearshore. Full details regarding this set-up can be found in Gallagher et al. (2016a).
We needed to limit the simulations to the following 30-year blocks: 1980–2009 and 2070–2099 for each available EC-Earth ensemble member, because of the computational weight of the high resolution nested simulations carried out using the WAVEWATCH III model. The comparisons referred to in this paper are between the future period 2070–2099 (for both RCP4.5 and RCP8.5) and the historical/industrial period 1980–2009.
The following nomenclature is used throughout this paper when referring to the ensemble members and the historical and future periods. Each ensemble member consists of an historical simulation and 2 future simulations (RCP4.5 and RCP8.5) and are denoted meiX, me4X and me8X where denotes the ensemble member, “i” refers to the historical or industrial period, 4 and 8 refer to RCP4.5 and RCP8.5 respectively and “me” denotes the fact that it is a Met Éireann ensemble member. This is also summarised in Table 1.
Table 1Table explaining the logic behind the experiment names used in this paper. The last number in the name refers to the ensemble member. The third letter identifies whether the data refer to the historical period (i) or were generated under RCP4.5 (4) or RCP8.5 (8). Under RCP4.5 greenhouse gas emissions are expected to peak around the year 2040 and decline after that. Under RCP8.5 greenhouse gas emissions are expected to increase throughout the 21st century.

We considered the first three modes of MSLP variability for a Northern Hemisphere region spanning 20–90∘ and 80∘ W–40∘ E using the 3-member EC-Earth ensemble consisting of 3 historical periods (mei1, mei2, mei3), 3 future periods under RCP4.5 (me41, me42, me43) and 3 future periods under RCP8.5 (me81, me82, me83). The months of December through to March were used in the calculations and analysis. For comparison, MSLP variability was also computed using the ERA-Interim reanalysis dataset.
We used Empirical Orthogonal Function (EOF) analysis to examine the variability in the EC-Earth MSLP fields for the periods mentioned above. This multivariate statistical technique is used in order to reduce the dimensionality of a dataset containing numerous related variables and at the same time retain as much variance as possible. It has been extensively applied to spatio-temporal datasets and it outputs a set of spatial patterns and associated time series, which typically account for a decreasing proportion of variability of the original data. The spatial variance patterns are orthogonal to each other and are termed EOFs. The one-dimensional time-series of the EOFs are referred to as Principal Component (PC) time-series. Here we used monthly mean gridded MSLP fields for December, January, February and March for each year in the 30-year periods (i.e. gridded files containing 120 months of MSLP data).
We used the Python eof library to calculate the EOFs and PCs using the EC-Earth MSLP data where the EOFs are expressed as a covariance between the PC time series and the MSLP anomalies at each grid point. The MSLP anomalies were computed using the 1864–1963 base period (NAO, 2018) of the relevant EC-Earth historical ensemble member. The same base period as in Gleeson et al. (2017) was used for consistency.
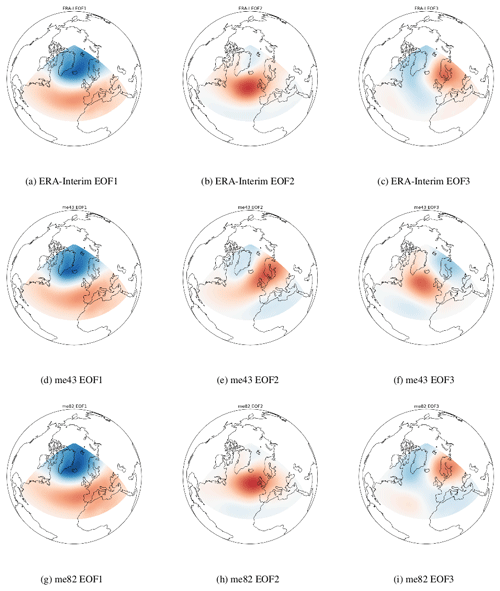
Figure 2The first three EOF patterns for ERA-Interim (a) to (c), EC-Earth me43 (d) to (f) and EC-Earth me82 (g) to (i).
Individual EOFs sometimes have a physical interpretation associated with them. In terms of MSLP in the Atlantic region, the first EOF refers to the NAO. The second and third EOFs refer to the EA or the SCAND patterns. In our calculations the NAO accounted for 35 %–46 % of the MSLP variability, the EA accounted for 15 %–20 % and the SCAND accounted for 10 %–15 %.
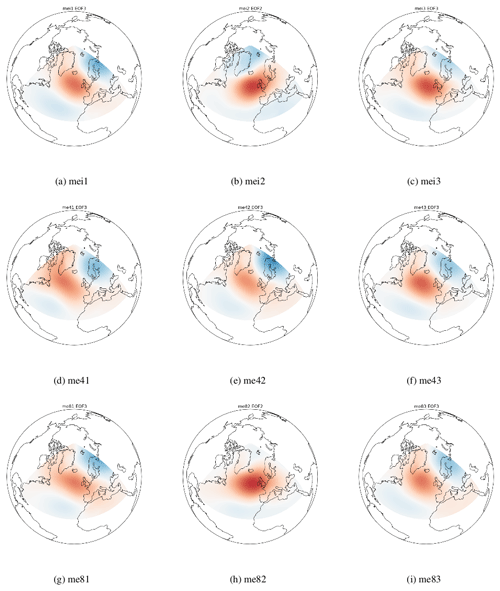
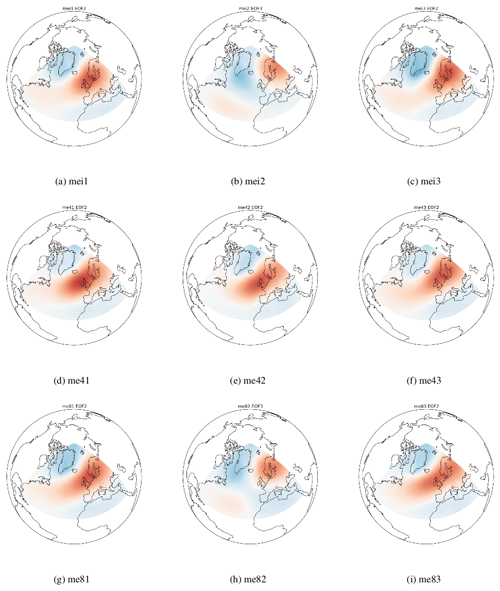
Sample EOF maps for the ERA-Interim dataset are shown in Fig. 2a to c. me43 and me82 are shown in Fig. 2d to f and g to i respectively. Note that the EOF2 of me43 corresponds to the SCAND pattern and EOF3 corresponds to the EA pattern and that the positive centre of the EA has a more northwesterly position than in ERA-Interim or me82. For some of the ensemble members it was more difficult to determine whether EOF2/3 corresponded to the EA or SCAND pattern. Figures A1 and A2 in the Appendix show the EA and SCAND patterns respectively for each historical, RCP4.5 and RCP8.5 ensemble member.
We evaluated means and extremes of the EC-Earth 10 m wind speeds using the ERA-Interim dataset, and the WAVEWATCH III outputs using buoy observations, scatterometer data and a historical WAVEWATCH III simulation driven by ERA-Interim fields. The biases are mostly within 10 %. The EC-Earth ensemble of projections suggests decreases of up to 14 % in the 95th percentile of 10 m wind speed over the North Atlantic by the end of the century for winter (DJF) under RCP8.5. In accordance, WAVEWATCH III suggests decreases in the 95th percentile of Hs of 5 %–10 % around Ireland by the end of the century. Further details on the evaluation of the winds from EC-Earth and the winds and waves from WAVEWATCH III are available in Gallagher et al. (2016a) and Gleeson et al. (2017).
In the following subsections we analyse the relationships between the 95th percentile of Hs and the PC time series associated with the NAO, EA and SCAND teleconnection patterns for the historical period 1980–2009 and the future period 2070–2099 under both RCP4.5 and RCP8.5 forcing scenarios. Spearman correlations are presented in Sect. 4.1 and 20-year return levels of Hs for different combinations of the NAO, EA and SCAND indices using extreme value theory are discussed in Sect. 4.2. 20 years return levels were used, following on from previous work by Gleeson et al. (2017). Other return periods can, of course, be calculated with the fitted model parameters.
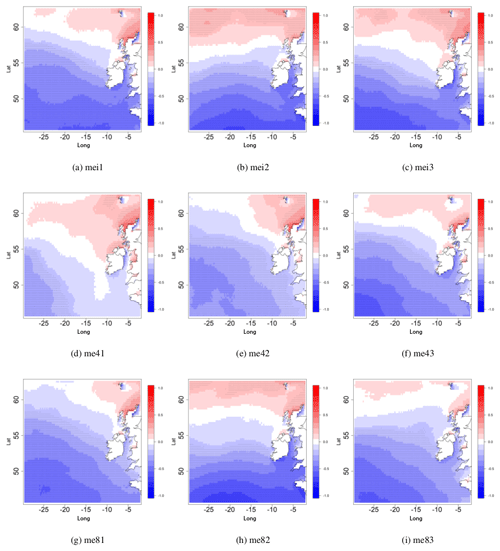
Figure 3The Spearman correlation coefficient between the EA index and the 95th percentile of Hs for DJFM. (a–c) historical period (1980–2009) 3× ensemble members; (d–f) future period 2070–2099 under RCP4.5 and similarly (g–h) is for 2070–2099 under RCP8.5. Correlations statistically significant at the α<0.05 level are dotted.
4.1 Correlations between the NAO, EA and SCAND and the 95th percentile of Hs
As in Gleeson et al. (2017), but with minor differences, the 95th percentile of Hs is positively correlated with the PC time-series associated with the NAO, with large areas west of Ireland where it exceeds +0.7. Figures 3 and 4 show the Spearman correlation coefficient between the PC time-series corresponding to the EA and the SCAND respectively and the 95th percentile of Hs for the months of December to March. In Figs. 3 and 4 the results shown in (a)–(c) are for the historical period and show each of the 3 ensemble members, (d)–(f) are for the future period under RCP4.5 and similarly (g)–(i) are for the future period under RCP8.5. Correlations which are statistically significant at the 0.05 level are dotted.
In Fig. 3 areas to the north of Ireland tend to mostly show a positive correlation between the PC corresponding to the EA and 95th percentile of Hs while around Ireland and to the south of the country, correlations are negative. This is consistent with the fact that EA in its negative phase is associated with a centre of low pressure in the North Atlantic west of Ireland and hence larger waves. Correlations of both sign increase further away from Ireland. Correlations are mostly statistically not significant around the north coast of Ireland.
Again in Fig. 4 the statistically significant correlations at the 95 % confidence limit are dotted. Correlations are mostly negative around Ireland and positive further north. This is consistent with the behaviour of the SCAND index. In its positive phase there is an area of high pressure extending from Scandinavia towards Europe with an area of low pressure around Greenland. Note that the SCAND pattern for mei2 and me82 (see Fig. A2) shows the area of low pressure around Greenland extending further south into the Atlantic than in the other ensemble members. The influence of this on the correlations between the PC time-series and the 95th percentile of Hs can be clearly seen in Fig. 4b and h where areas of positive correlation extend much further south.
4.2 The NAO, EA and SCAND teleconnections vs 20-year return levels of Hs
The Generalised Extreme Value (GEV) distribution may be used to calculate the extremes of a dataset (Coles, 2001). The maxima of blocks of data (for example monthly or annual) may be modelled with the distribution function given by
The three parameters in the distribution are the shape , the location and the scale σ>0. Having fitted the parameters to a given dataset, the distribution function above in Eq. (1) may be inverted to yield N-year return levels; that is, the value that has a 1∕N probability of being exceeded in a given year, given by
In this work we applied the GEV to the DJFM monthly maxima of the Hs data described above. The model was fitted with maximum likelihood (ML) inference using the ismev package in R (http://CRAN.R-project.org/package=ismev, last access: 18 March 2019). The parameters in the GEV are often allowed to be non-stationary. For instance, linear or harmonic dependence in time may be included to model long-term trends or seasonality in extremes; see, for example, Caires et al. (2006), Clancy et al. (2015), Izaguirre et al. (2011). In Gleeson et al. (2017), the GEV model was applied to the present dataset with station-based NAO used as a covariate for the location and scale parameters.
In this present work, we allowed the location parameter to depend on the three PCs: . The shape and scale parameters were kept constant, as was the case in Izaguirre et al. (2011). With such a model, we see from Eq. (2) that any overall increase (decrease) in μ will result in higher (lower) return levels of extremes.
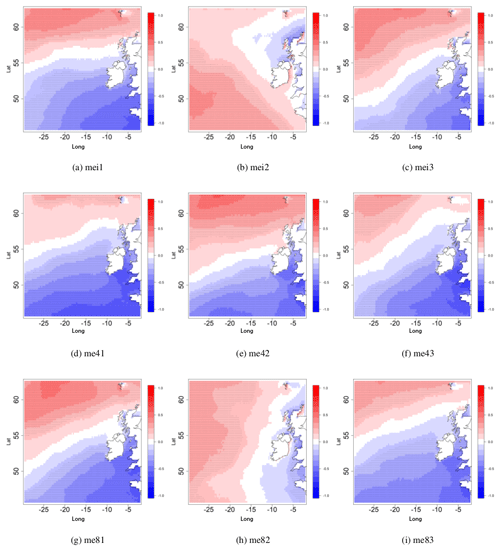
Figure 4The Spearman correlation coefficient between the SCAND index and the 95th percentile of Hs for DJFM. (a–c) historical period (1980–2009) 3× ensemble members; (d–f) future period 2070–2099 under RCP4.5 and similarly (g–h) is for 2070–2099 under RCP8.5. Correlations statistically significant at the α<0.05 level are dotted.
In all ensemble members for both historical and future scenarios, the ML estimate of μ1, relating to the NAO (PC1), was found to be non-negative throughout the domain. Thus, a positive phase of the NAO may contribute to an increase in extremes of Hs. This effect of the NAO was discussed in detail in Gleeson et al. (2017), and in particular how this is expected to vary under the two future scenarios. Here we focus on the EA and SCAND. In Figs. B1 and B2 in the Appendix we show the ML estimates of μ2 and μ3, respectively. Each ensemble member is shown for the historical and two future periods. Note the similarities, as expected, between the correlation maps in Fig. 3 and the spatial distribution of μ2 in Fig. B1 and similarly between Figs. 4 and B2 for the SCAND and the distribution of μ3.
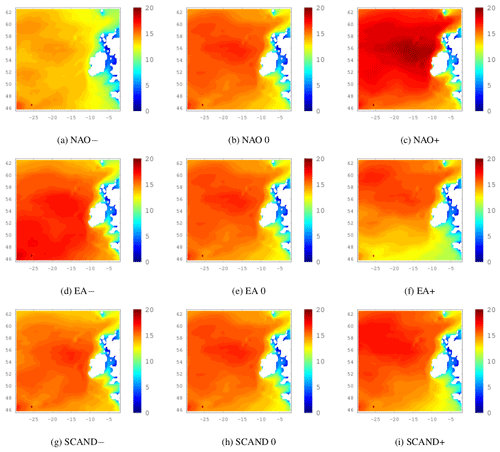
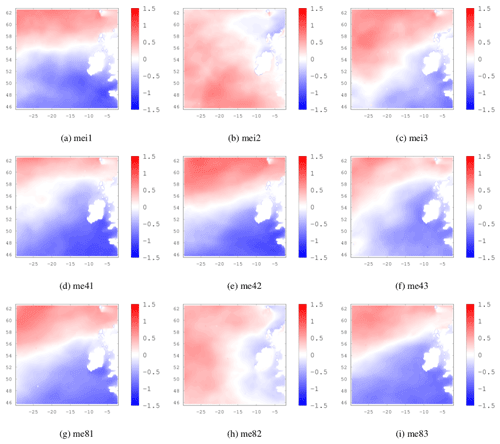
Figure 520-year return levels of Hs where the effects of the NAO, EA and SCAND are isolated by setting each of the remaining two indices to zero. The ensemble mean is shown for the historical simulations.
The remainder of this section is dedicated to the influence of the NAO, EA and SCAND indices on 20-year return levels of Hs. Varying the NAO from −2 to 0 to +2, while keeping the EA and SCAND in a neutral state of zero, shows a clear increase in the 20-year return levels of Hs when the NAO is in its positive phase. This is shown in Fig. 5a–c where the ensemble means of the 3 members for the historical period are shown. Corresponding results under RCP4.5 and RCP8.5 are shown in Fig. C1 in the Appendix. The effect of the NAO is clear and robust throughout the datasets; both for the historical period and the RCP scenario simulations, return levels increase significantly when the NAO is positive and are lower when the NAO is negative or zero. This coincides well with the known effects of the NAO in enhancing the westerlies in the North Atlantic and positioning of the jet stream and therefore the storm track, towards the west coast of Ireland.
In comparison to the NAO, the influence of the EA and SCAND indices on Hs over our domain is much smaller (Fig. 5). Figures C2 and C3 in the Appendix show the corresponding EA and SCAND 20-year return level plots under RCP4.5 and RCP8.5 forcings. When the EA index becomes positive, the 20-year return levels of Hs decrease in the south of the study domain in particular and the higher wave heights seem to be “pushed further north”. The decrease in wave heights south of Ireland is consistent with the centre of positive MSLP anomalies that characterises the EA pattern. The negative effect of a positive-phase EA on 20-year return levels of Hs is also observed in the RCP simulations.
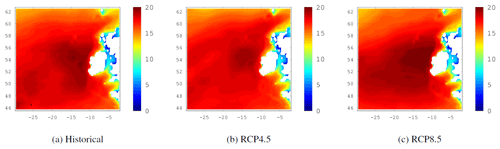
Figure 6Ensemble mean 20-year return levels of Hs where the NAO is set to +2 and both the EA and SCAND are −2. A positive phase NAO and negative phase EA and SCAND is associated with the highest waves off Ireland.
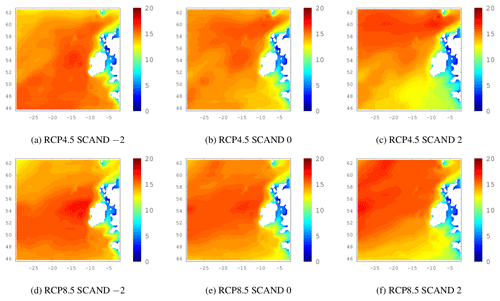
Figure 5g to i shows the isolated effect of the SCAND pattern on 20-year return levels of Hs by keeping the NAO and the EA indices set to values of 0. The effect is more difficult to see in the ensemble mean of the historical simulations but is clear in the RCP4.5/8.5 SCAND plots in Fig. C3 in the Appendix. As mentioned earlier, the SCAND pattern in mei2 has the area of low pressure over Greenland extending further south than in the other 2 ensemble members and makes the effect of the SCAND pattern on wave heights more difficult to see. As the SCAND index goes from a positive to a negative phase, 20-year return levels of Hs decrease in the southeast of the domain but seem to increase in the north, for the historical period as well as for the RCPs. The SCAND is associated with easterly winds from a blocking anticyclonic set-up over Scandinavia and is known to divert the Atlantic jet stream east of its climatological position (Bueh and Nakamura, 2007). The physical effects we see here are consistent with the known climatic impacts of the SCAND pattern.
Ensemble means of the 20-year return levels of Hs are shown in Fig. 6 for the historical period and future periods under RCP4.5 and RCP8.5 where the NAO index is +2 and the EA and SCAND indices are set to −2. Of the three teleconnections, the NAO has the strongest influence on extreme waves in the northeast Atlantic, followed by the EA with the SCAND having the smallest influence. Figure 6c clearly shows that under RCP8.5 in particular the 20-year return levels of Hs may increase off the west coast of Ireland despite a prediction of an overall decreasing trend in mean wind speeds and thus waves.
We analysed principal component time-series associated with the NAO, EA and SCAND teleconnection patterns computed using an ensemble of global EC-Earth climate projections and the influence of these patterns on regional wave projections over the North Atlantic. The influence of the NAO on extreme waves is greater than that of the EA and SCAND teleconnection patterns. We found that the 20-year return levels of Hs are largest when the NAO is in a strong positive phase (e.g. +2) and the EA and SCAND are in strong negative phases (e.g. −2). During the positive phase of the NAO the pressure gradient over the North Atlantic increases due to strengthening of the Icelandic Low and Azores High. Stronger westerly winds, associated with the increased pressure gradient, also generate larger waves. The East Atlantic pattern, in its negative phase, has a centre of negative MSLP anomalies over the eastern North Atlantic, roughly between the two centres of the NAO. This is also associated with stronger winds and therefore larger waves. The negative phase of the SCAND pattern has a negative pole of MSLP anomalies centered over Scandinavia. When the NAO is in a positive phase, the SCAND pattern enhances the westerly winds over the Atlantic which in turn has a positive impact on wave heights off the west coast of Ireland. This is why the +, −, − patterns for the NAO, EA and SCAND respectively are assoicated with the largest significant wave heights as found in this study. Gleeson et al. (2017) showed that local increases in extreme waves are possible in the future under RCP8.5. The results presented here are consistent with this but also include the effects of the EA and SCAND whose centres of action modulate the influence of the NAO on Hs.
The running of CMIP6 climate simulations is currently in progress and we plan to repeat the analysis by carrying out new multi-model global climate simulations and downscaled simulations. It is also worth noting that the second and third EOF patterns vary quite a lot. Having a larger ensemble size would be of benefit and would make the results more robust. In addition, we used two 30-year periods 1980–2009 and 2070–2099. The analysis would also benefit from using rolling 30-year periods. In addition we are currently doing a separate analysis of the wave energy flux and wave period.
Although climate projections suggest that Hs and wave energy flux will decrease on average in the Northeast Atlantic Ocean by the end of the century, extremes will still occur and may be enhanced depending on the phase of large-scale patterns such as the NAO, EA and SCAND.
The datasets have been archived at Met Éireann. There is currently no publicly available method for data access so the Met Éireann should be contacted for dataset access.
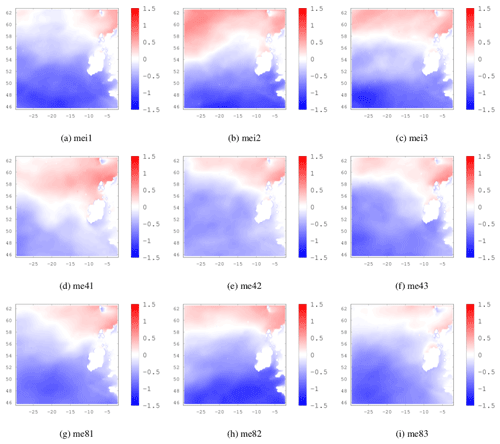
Figure B1Maximum likelihood estimate of the μ2 parameter. The three ensemble members are shown for the historical period (a) to (c), future period under RCP4.5 (d) to (f), and future period under RCP8.5 (g) to (i).
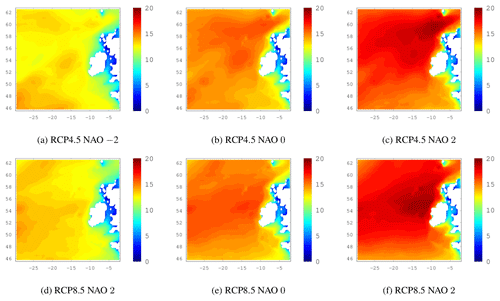
Figure C120-year return levels of Hs. The NAO index varies from 3 values of the NAO index while the EA and SCAND are held in their neutral state (zero). The top row shows the ensemble mean for the future period under RCP4.5 and the bottom row is similar but shows RCP8.5 results.
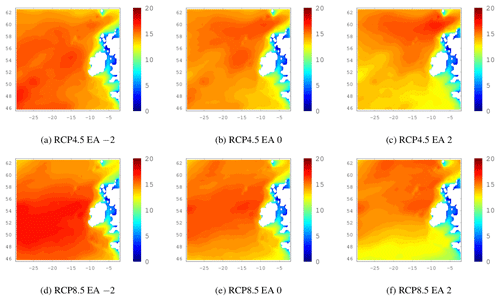
Figure C220-year return levels of Hs. The EA index varies from 3 values of the NAO index while the NAO and SCAND are held in their neutral state (zero). The top row shows the ensemble mean for the future period under RCP4.5 and the bottom row is similar but shows RCP8.5 results.
EG ran the EC-Earth global climate simulations, analysed the wind outputs and computed the PC time-series using EC-Earth data; SG ran the WAVEWATCH III simulations using EC-Earth boundary conditions, JJ analysed the wave outputs and correlations between significant wave height and the PC time-series; CC did a statistical analysis of extreme waves and the PC time-series using a Generalised Extreme Value distribution. EG, CC and LZ analysed the outputs of the statistical tests. EG and CC prepared the manuscript and received contributions from JJ, LZ, FD and SG.
The authors declare that they have no conflict of interest.
This article is part of the special issue “18th EMS Annual Meeting: European Conference for Applied Meteorology and Climatology 2018”. It is a result of the EMS Annual Meeting: European Conference for Applied Meteorology and Climatology 2018, Budapest, Hungary, 3–7 September 2018.
The authors wish to acknowledge Roxana Tiron who helped to run the wave simulations and the EC-Earth community for useful discussions on principal component analysis outputs. The numerical simulations were performed on the Fionn cluster at the Irish Centre for High-end Computing (ICHEC) and at the Swiss National Computing Centre under the PRACE-2IP project (FP7 RI-283493) “Nearshore wave climate analysis of the west coast of Ireland”. The authors would like to thank the reviewers for their useful comments and feedback.
This paper was edited by Sandro Carniel and reviewed by Angela Pomaro and one anonymous referee.
Ardhuin, F., Rogers, E., Babanin, A. V., Filipot, J.-F., Magne, R., Roland, A., van der Westhuysen, A., Queffeulou, P., Lefevre, J.-M., Aouf, L., and Collard, F.: Semiempirical Dissipation Source Functions for Ocean Waves. Part I: Definition, Calibration, and Validation, J. Phys. Oceanogr., 40, 1917–1941, https://doi.org/10.1175/2010JPO4324.1, 2010. a
Atan, R., Goggins, J., and Nash, S.: A Detailed Assessment of the Wave Energy Resource at the Atlantic Marine Energy Test Site, Energies, 9, 967, https://doi.org/10.3390/en9110967, 2016. a, b
Barnston, A. and Livezey, E.: Classification, seasonality and persistence of low-frequency atmospheric circulation patterns, Mon. Weather Rev., 115, 1083–1126, 1987. a, b
Bertin, X., Prouteau, E., and Letetrel, C.: A significant increase in waveheight in the North Atlantic Ocean over the 29th century, Global Planet. Change, 106, 77–83, 2013. a
Bueh, C. and Nakamura, H.: Scandinavian pattern and its climatic impact, Q. J. Roy. Meteor. Soc., 133, 2117–2131, https://doi.org/10.1002/qj.173, 2007. a
Caires, S., Swail, V. R., and Wang, X. L.: Projection and analysis of extreme wave climate, J. Climate, 19, 5581–5605, 2006. a
Charles, E., Idier, D., Thiébot, J., Le Cozannet, G., Pedreros, R., Ardhuin, F., and Planton, S.: Present Wave Climate in the Bay if Biscay: Spatiotemporal Variability and Trends from 1958 to 2001, J. Climate, 25, 2020–2039, 2012. a
Clancy, C., Belissen V, Tiron, R., Gallagher, S., and Dias, F.: Spatial variability of extreme sea states on the Irish west coast, in: Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St John's, NL, Canada, 2015. a
Coles, S.: An introduction to statistical modeling of extreme values, Springer-Verlag London, 2001. a
Comas-Bru, L. and McDermott, F.: Impacts of the EA and SCA patterns on the European twentieth century NAO-winter climate relationship, Q. J. Roy. Meteor. Soc., 140, 354–363, https://doi.org/10.1002/qj.2158, 2014. a
Dodet, G., Bertin, X., and Taborda, R.: Wave climate variability in the North-East Atlantic Ocean over the last six decades, Ocean Model., 31, 120–131, 2010. a
Fichefet, T. and Maqueda, M.: Sensitivity of a global sea ice model to the treatment of ice thermodynamics and dynamics, J. Geophys. Res.-Oceans, 102, 12609–12646, 1997. a
Gallagher, S., Tiron, R., and Dias, F.: A detailed investigation of the nearshore wave climate and the nearshore wave energy resource on the west coast of Ireland, in: Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering OMAE, American Society of Mechanical Engineers, Nantes, France, https://doi.org/10.1115/OMAE2013-10719, 2013. a
Gallagher, S., Tiron, R., and Dias, F.: A long-term nearshore wave hindcast for Ireland: Atlantic and Irish Sea coasts (1979–2012), Ocean Dynam., 64, 1163–1180, https://doi.org/10.1007/s10236-014-0728-3, 2014. a
Gallagher, S., Gleeson, E., Tiron, R., McGrath, R., and Dias, F.: Wave climate projections for Ireland for the end of the 21st century including analysis of EC-Earth winds over the North Atlantic Ocean, Int. J. Climatol., 36, 4592–4607, https://doi.org/10.1002/joc.4656, 2016a. a, b, c
Gallagher, S., Tiron, R., Whelan, E., Gleeson, E., Dias, F., and McGrath, R.: The nearshore wind and wave energy potential of Ireland: A high resolution assessment of availability and accessibility, Renew. Energ., 88, 494–516, https://doi.org/10.1016/j.renene.2015.11.010, 2016b. a
Gleeson, E., McGrath, R., and Treanor, M.: Ireland's climate: the road ahead, Met Éireann, Dublin, Ireland, 2013. a
Gleeson, E., Gallagher, S., Clancy, C., and Dias, F.: NAO and extreme ocean states in the Northeast Atlantic Ocean, Adv. Sci. Res., 14, 23–33, https://doi.org/10.5194/asr-14-23-2017, 2017. a, b, c, d, e, f, g, h, i, j, k, l, m
Greatbatch, R. J.: The North Atlantic Oscillation, Stoch. Env. Res. Risk A., 14, 213–242, 2000. a
Hazeleger, W., Severijns, C., Semmler, T., Ştefănescu, S., Yang, S., Wang, X., Wyser, K., Dutra, E., Baldasano, J., Bintanja, R., Bougeault, P., Caballero, R., Ekman, A. M. L., Christensen, J. H., van den Hurk, B., Jimenez, P., Jones, C., Kållberg, P., Koenigk, T., McGrath, R., Miranda, P., Van Noije, T., Palmer, T., Parodi, J., Schmith, T., Selten, F., Storelvmo, T., Sterl, A., Tapamo, H., Vancoppenolle, M., Viterbo, P., and Willén, U.: EC-Earth: A Seamless Earth-System Prediction Approach in Action, B. Am. Meteor. Soc., 91, 1357–1363, https://doi.org/10.1175/2010BAMS2877.1, 2010. a, b, c
Hazeleger, W., Wang, X., Severijns, C., Ştefănescu, S., Bintanja, R., Sterl, A., Wyser, K., Semmler, T., Yang, S., van den Hurk, B., van Noije, T., van der Linden, E., and van der Wiel, K.: EC-Earth V2.2: description and validation of a new seamless earth system prediction model, Clim. Dynam., 39, 2611–2629, https://doi.org/10.1007/s00382-011-1228-5, 2012. a, b, c
Hurrell, J.: Decadal trends in the North Atlantic Oscillation: regional temperatures and precipitation, Oceanographic Literature Review, 2, 116, https://doi.org/10.1126/science.269.5224.676, 1996. a, b
Izaguirre, C., Mendez, F. J., Menendez, M., Luceño, A., and Losada, I. J.: Extreme wave climate variability in southern Europe using satellite data, J. Geophys. Res.-Oceans, 115, https://doi.org/10.1029/2009JC005802, 2010. a
Izaguirre, C., Méndez, F. J., Menéndez, M., and Losada, I. J.: Global extreme wave height variability based on satellite data, Geophys. Res. Lett., 38, 1–6, 2011. a, b
Janssen, P. A.: Progress in ocean wave forecasting, J. Comput. Phys., 227, 3572–3594, 2008. a
Komen, G. J., Cavaleri, L., Donelan, M., Hasselmann, K., Hasselmann, S., and Janssen, P.: Dynamics and modelling of ocean waves, Cambridge university press, 1994. a
Madec, G.: Nemo ocean engine: Note du pole de modélisation, Institut Pierre-Simon Laplace (IPSL), France, No 27 ISSN No 1288–1619, 2008. a
NAO: The Climate Data Guide: Hurrell North Atlantic Oscillation (NAO) Index (station-based), available at: https://climatedataguide.ucar.edu/climate-data/hurrell-north-atlantic-oscillation-nao-index-station-based, last acces: 28 November 2018. a
Pokorná, L. and Huth, R.: Climate impacts of the NAO are sensitive to how the NAO is defined, Theor. Appl. Climatol., 119, 639–652, 2015. a
Roland, A.: Development of WWM II: Spectral wave modelling on unstructured meshes, PhD thesis, Institute of Hydraulics and Wave Resource Engineering, Technical University Darmstadt, Germany, 2008. a
Santo, H., Taylor, P., Taylor, R. E., and Stansby, P.: Decadal variability of wave power production in the North-East Atlantic and North Sea for the M4 machine, Renew. Energ., 91, 442–450, https://doi.org/10.1016/j.renene.2016.01.086, 2016a. a
Santo, H., Taylor, P. H., and Gibson, R.: Decadal variability of extreme wave height representing storm severity in the northeast Atlantic and North Sea since the foundation of the Royal Society, P. R. Soc. A, 472, https://doi.org/10.1098/rspa.2016.0376, 2016b. a
Scherrer, S. C., Croci-Maspoli, M., Schwierz, C., and Appenzeller, C.: Two-dimensional indices of atmospheric blocking and their statistical relationship with winter climate patterns in the Euro-Atlantic region, Int. J. Climatol., 26, 233–250, 2006. a
Taylor, K. E., Stouffer, R. J., and Meehl, G. A.: An overview of CMIP5 and the experiment design, B. Am. Meteor. Soc., 93, 485–498, 2012. a, b
Tolman, H.: User manual and system documentation of Wavewatch III version 4.18, Tech. Rep. 316, NOAA/NWS/NCEP/MMAB, 2014. a, b
Trigo, R. M., Valente, M. A., Trigo, I. F., Miranda, P. M. A., Ramos, A. M., Paredes, D., and García-Herrera, R.: The Impact of North Atlantic Wind and Cyclone Trends on European Precipitation and Significant Wave Height in the Atlantic, Ann. NY Acad. Sci., 1146, 212–234, https://doi.org/10.1196/annals.1446.014, 2008. a
Valcke, S.: OASIS3 user guide (prism_2-5), PRISM support initiative report, 3, 64, 2006. a
van Loon, H. and Rogers, J. C.: The seesaw in winter temperatures between Greenland and northern Europe. Part I: General description, Mon. Weather Rev., 106, 296–310, 1978. a
Vautard, R.: Multiple Weather Regimes over the North Atlantic: Analysis of Precursors and Successors, Mon. Weather Rev., 118, 2056–2081, https://doi.org/10.1175/1520-0493(1990)118<2056:MWROTN>2.0.CO;2, 1990. a
Wallace, J. M. and Gutzler, D. S.: Teleconnections in the Geopotential Height Field during the Northern Hemisphere Winter, Mon. Weather Rev., 109, 784–812, https://doi.org/10.1175/1520-0493(1981)109<0784:TITGHF>2.0.CO;2, 1981. a
Wang, X. and Swail, V.: Changes of extreme wave heights in Northern Hemisphere oceans and related atmospheric circulation regimes, J. Climate, 14, 2204–2221, 2001. a
Wang, X. and Swail, V.: Trends of Atlantic wave extremes as simulated in a 40-year wave hindcast using kinematically reanalysed wind fields, J. Climate, 15, 1020–1035, 2002. a
Woollings, T. and Blackburn, M.: The North Atlantic Jet Stream under Climate Change and Its Relation to the NAO and EA Patterns, J. Climate, 25, 886–902, https://doi.org/10.1175/JCLI-D-11-00087.1, 2012. a
Zubiate, L., McDermott, F., Sweeney, C., and O'Malley, M.: Spatial variability in winter NAO-wind speed relationships in western Europe linked to concomitant states of the East Atlantic and Scandinavian patterns, Q. J. Roy. Meteor. Soc., 143, 552–562, https://doi.org/10.1002/qj.2943, 2017. a
- Abstract
- Introduction
- Models
- Atmospheric teleconnections
- Analysis and results
- Conclusions
- Data availability
- Appendix A: EA and SCAND Patterns
- Maximum likelihood estimate of the μ2 and μ3 parameters
- 20-year return levels of Hs for varying values of the NAO, EA and SCAND indices
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Review statement
- References
- Abstract
- Introduction
- Models
- Atmospheric teleconnections
- Analysis and results
- Conclusions
- Data availability
- Appendix A: EA and SCAND Patterns
- Maximum likelihood estimate of the μ2 and μ3 parameters
- 20-year return levels of Hs for varying values of the NAO, EA and SCAND indices
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Review statement
- References